前言
用通俗易懂的语言描述一些教科书的理论知识,确实是个力气活。
以下内容只需要有初中数学方程的知识即可。
以下各种符号,各种理论,你可以不必记住,但是必须要知道什么样的数据,调用sklearn 中的哪些函数.
1、最小二乘法: 本质是求解多个测量值的最小误差, 利用的是求导的方法
上栗子:
小明是跑运输的,跑1公里需要6块,跑2公里需要5块(那段时间刚好油价跌了),跑3公里需要7块,跑4公里需要10块,请问跑5公里需要多少块?如果我们有初中数学基础,应该会自然而然地想到用线性方程组来做,对吧。
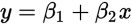
这里假定x是公里数,y是运输成本(β1和β2是要求的系数)。我们把上面的一组数据代入得到这么几个方程:
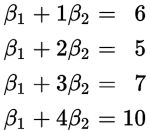
如果存在这样的β1和β2,让所有的数据(x,y)=(1,6),(2,5),(3,7),(4,10)都能满足的话,那么解答就很简单了,β1+5β2就是5公里的成本,对吧。
但遗憾的是,这样的β1和β2是不存在的,上面的方程组很容易,你可以把前面两个解出来得到一组β1和β2,后面两个也解出来同样得到一组β1和β2。这两组β1和β2是不一样的。
形象地说,就是你找不到一条直线,穿过所有的点,因为他们不在一条直线上。如下图:

可是现实生活中,我们就希望能找到一条直线,虽然不能满足所有条件,但能近似地表示这个趋势,或者说,能近似地知道5公里的运输成本,这也是有意义的。
现实生活当中,有很多这样的例子,想起以前在某公司上班的时候,CEO说我们研发部做事有个问题:一个研发任务,要求三个月做完,因为周期太短,完成不了,就干脆不做,这显然是不对的,要尽全力,哪怕三个月完成了80%,或者最终4个月完成,总比不作为的好。
其实最小二乘法也是这样,要尽全力让这条直线最接近这些点,那么问题来了,怎么才叫做最接近呢?直觉告诉我们,这条直线在所有数据点中间穿过,让这些点到这条直线的误差之和越小越好。这里我们用方差来算更客观。也就是说,把每个点到直线的误差平方加起来:

(如果上面的四个方程都能满足,那么S的值显然为0,这是最完美的,但如果做不到完美,我们就让这个S越小越好)
接下来的问题就是,如何让这个S变得最小。这里有一个概念,就是求偏导数
要让S取得最小值(或最大值,但显然这个函数没有最大值,自己琢磨一下),那么S对于β1和β2分别求偏导结果为0,用一个直观的图来表示:
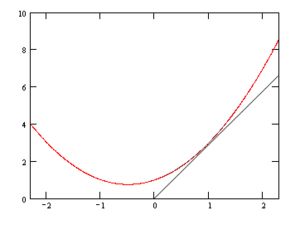
我们看到这条曲线,前半部分是呈下降的趋势,也就是变化率(导数)为负的,后半部分呈上升的趋势,也就是变化率(导数)为正,那么分界点的导数为0,也就是取得最小值的地方。这是一个变量的情况,对于多个变量的情况,要让S取得最小值,那最好是对β1和β2分别求导(对β1求导的时候,把β2当常量所以叫求偏导),值为0:

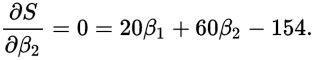
看到这个我们就熟悉了,两个变量,刚好有两个方程式,初中学过,那么很容易得出:
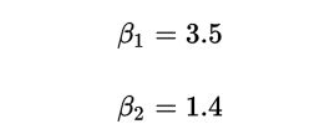
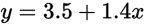
这个函数也就是我们要的直线,这条直线虽然不能把那些点串起来,但它能最大程度上接近这些点。也就是说5公里的时候,成本为3.5+1.4x5=10.5块,虽然不完美,但是很接近实际情况
2、导数:
上栗子
导数是什么,无非就是变化率呗,王小二今年卖了100头猪,去年卖了90头,前年卖了80头。。
变化率或者增长率是什么?每年增长10头猪,多简单。这里需要注意有个时间变量---年。王小二卖猪的增长率是10头/年,也就是说,导数是10。
函数y=f(x)=10x+30,这里我们假设王小二第一年卖了30头,以后每年增长10头,x代表时间(年),y代表猪的头数
当然,这是增长率固定的情形,现实生活中,很多时候,变化量也不是固定的,也就是说增长率也不是恒定的。
比如,函数可能是这样: y=f(x)=5x²+30,这里x和y依然代表的是时间和头数,不过增长率变了
变化率或者增长率是什么?每年增长10头猪,多简单。这里需要注意有个时间变量---年。王小二卖猪的增长率是10头/年,也就是说,导数是10。
函数y=f(x)=10x+30,这里我们假设王小二第一年卖了30头,以后每年增长10头,x代表时间(年),y代表猪的头数
当然,这是增长率固定的情形,现实生活中,很多时候,变化量也不是固定的,也就是说增长率也不是恒定的。
比如,函数可能是这样: y=f(x)=5x²+30,这里x和y依然代表的是时间和头数,不过增长率变了
3、偏导数: 当变量超过一个的时候,对其中一个变量求变化率
上栗子
深度学习还有一个重要的数学概念:偏导数,偏导数的偏怎么理解?偏头疼的偏,还是我不让你导,你偏要导?都不是,我们还以王小二卖猪为例,刚才我们讲到,x变量是时间(年),可是卖出去的猪,不光跟时间有关啊,随着业务的增长,王小二不仅扩大了养猪场,还雇了很多员工一起养猪。所以方程式又变了:y=f(x)=5x₁²+8x₂ + 35x₃ +30
这里x₂代表面积,x₃代表员工数,当然x₁还是时间。上面我们讲了,导数其实就是变化率,那么偏导数是什么?偏导数无非就是多个变量的时候,针对某个变量的变化率呗。在上面的公式里,如果针对x₃求偏导数,也就是说,员工对于猪的增长率贡献有多大,或者说,随着(每个)员工的增长,猪增加了多少,这里等于35---每增加一个员工,就多卖出去35头猪. 计算偏导数的时候,其他变量都可以看成常量,这点很重要,常量的变化率为0,所以导数为0,所以就剩对35x₃ 求导数,等于35. 对于x₂求偏导,也是类似的。
这里x₂代表面积,x₃代表员工数,当然x₁还是时间。上面我们讲了,导数其实就是变化率,那么偏导数是什么?偏导数无非就是多个变量的时候,针对某个变量的变化率呗。在上面的公式里,如果针对x₃求偏导数,也就是说,员工对于猪的增长率贡献有多大,或者说,随着(每个)员工的增长,猪增加了多少,这里等于35---每增加一个员工,就多卖出去35头猪. 计算偏导数的时候,其他变量都可以看成常量,这点很重要,常量的变化率为0,所以导数为0,所以就剩对35x₃ 求导数,等于35. 对于x₂求偏导,也是类似的。
求偏导我们用一个符号 表示:比如 y/ x₃ 就表示y对 x₃求偏导。
4、简单线性回归
上栗子
我们以房屋面积(x)与房屋价格(y)为例,显而易见,这两者是一种线性关系,房屋价格正比于房屋面积,我们假设比例为w:
y^ = w * x
然而,这种线性方程一定是过原点的,即当x=0时,y也一定为0。这可能并不符合现实中的某些场景。
为了能够让方程具有更广泛的适应性,我们这里再增加一个截距,设为b,即:y^ = w * x + b
这个方程就是我们数据建模的模型。方程中的w和b就是模型的参数。
假定数据集数据如下:

线性回归是用来解释自变量和因变量之间的关系,但是,这种关系并非严格的函数映射关系。从数据集中,我们也看到了这一点。相同面积的房屋,价格并不完全相同,但是,也不会相差太大。
什么是严格的函数映射关系?
指的是x 相同,y一定是相同的。
5、多元线性回归
上栗子
现实生活中数据可能是比较复杂的,自变量也很可能不是一个。
例如:影响房屋价格可能不止房屋面积一个因素,可能还有楼层,距地铁站的距离,距市中心的距离,房间数量等等。不过,这些因素对房屋价格影响的力度(权重)是不同的,例如:房屋所在楼层对房屋价格的影响就远不及房屋的面积,因此,我们可以使用多个权重来表示多个因素与房屋的关系:
g(x) = w1x1 + w2x2 + w3x3 + w4x4 +b
x1,x2,x3,x4 :影响因素,及特征,也是字段(Excel里的列名)
w1,w2,w3,...,wn : 每个X影响的力度
化简:把b替换成w0,并让他乘以x0,让x0 =1.
g(x) = w1x1 + w2x2 + w3x3 + w4x4 +w0x0

# linear_model模块可实现各种线性模型。
from sklearn import linear_model
# 创建一个线性回归模型
reg = linear_model.LinearRegression()
# fit :拟合线性回归模型
reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
# 线性回归函数公式:
# g(x) = w1x1 + w2x2 + w3x3 + w4x4 + w0
reg.coef_ # #获取斜率w1,w2,w3,...,wn
reg.intercept_#获取截距w0
6、官方完整案例代码:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# 加载糖尿病数据集
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
# 仅使用一个特征(字段)
diabetes_X = diabetes_X[:, np.newaxis, 2]
# 将数据分隔成训练集
diabetes_X_train = diabetes_X[:-20]
# 将数据分隔成测试集合
diabetes_X_test = diabetes_X[-20:]
# 将目标分为训练/测试集
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
# 创建线性回归对象
regr = linear_model.LinearRegression()
# 使用训练集训练模型
regr.fit(diabetes_X_train, diabetes_y_train)
# 使用测试集进行预测
diabetes_y_pred = regr.predict(diabetes_X_test)
# 系数
print('Coefficients: n', regr.coef_)
# 均方误差
print('Mean squared error: %.2f'
% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# 确定系数:1为完美预测
print('Coefficient of determination: %.2f'
% r2_score(diabetes_y_test, diabetes_y_pred))
# 绘图输出
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
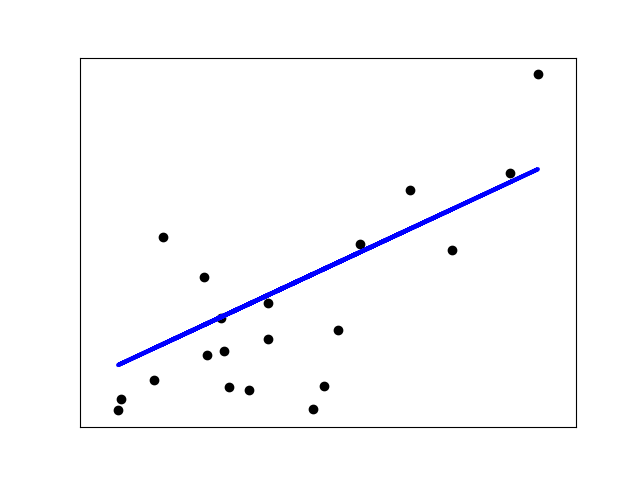
生成的结果:
参考:
1、https://www.zhihu.com/question/36324957/answer/255970074
2、https://scikit-learn.org/stable/user_guide.html
2、https://scikit-learn.org/stable/user_guide.html
 同乐学堂
同乐学堂
 微信扫一扫,打赏作者吧~
微信扫一扫,打赏作者吧~


