Tensor 张量意义 

• 张量有多种. 零阶张量为 纯量或标量 (scalar) 也就是一个数值. 比如 [1]
• 一阶张量为 向量 (vector), 比如 一维的 [1, 2, 3]
• 二阶张量为 矩阵 (matrix), 比如 二维的 [[1, 2, 3],[4, 5, 6],[7, 8, 9]]
• 以此类推, 还有 三阶 三维的 …

创建数据 

搭建模型 

计算误差 

传播误差 

训练 

Session 会话控制

简单运用 

Variable 变量

简单运用 

Placeholder 传入值

简单运用 

什么是激励函数 (Activation Function)

非线性方程 

说到线性方程, 我们不得不提到另外一种方程, 非线性方程 (nonlinear function). 我们假设, 女生长得越漂亮, 越多男生爱. 这就可以被当做一个线性问题. 但是如果我们假设这个场景是发生在校园里. 校园里的男生数是有限的, 女生再漂亮, 也不可能会有无穷多的男生喜欢她. 所以这就变成了一个非线性问题.再说..女生也不可能是无穷漂亮的. 这个问题我们以后有时间私下讨论.

然后我们就可以来讨论如何在神经网络中达成我们描述非线性的任务了. 我们可以把整个网络简化成这样一个式子. Y = Wx, W 就是我们要求的参数, y 是预测值, x 是输入值. 用这个式子, 我们很容易就能描述刚刚的那个线性问题, 因为 W 求出来可以是一个固定的数. 不过这似乎并不能让这条直线变得扭起来 , 激励函数见状, 拔刀相助, 站出来说道: “让我来掰弯它!”.

激励函数 

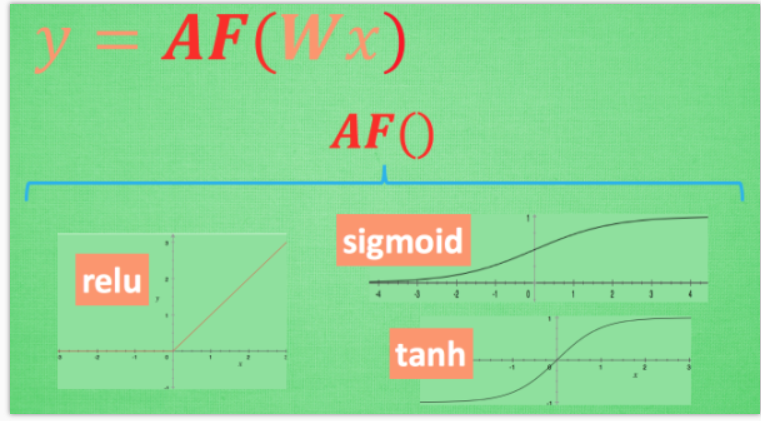
这里的 AF 就是指的激励函数. 激励函数拿出自己最擅长的”掰弯利器”, 套在了原函数上 用力一扭, 原来的 Wx 结果就被扭弯了.

其实这个 AF, 掰弯利器, 也不是什么触不可及的东西. 它其实就是另外一个非线性函数. 比如说relu, sigmoid, tanh. 将这些掰弯利器嵌套在原有的结果之上, 强行把原有的线性结果给扭曲了. 使得输出结果 y 也有了非线性的特征. 举个例子, 比如我使用了 relu 这个掰弯利器, 如果此时 Wx 的结果是1, y 还将是1, 不过 Wx 为-1的时候, y 不再是-1, 而会是0.

你甚至可以创造自己的激励函数来处理自己的问题, 不过要确保的是这些激励函数必须是可以微分的, 因为在 backpropagation 误差反向传递的时候, 只有这些可微分的激励函数才能把误差传递回去.

常用选择 

想要恰当使用这些激励函数, 还是有窍门的. 比如当你的神经网络层只有两三层, 不是很多的时候, 对于隐藏层, 使用任意的激励函数, 随便掰弯是可以的, 不会有特别大的影响. 不过, 当你使用特别多层的神经网络, 在掰弯的时候, 玩玩不得随意选择利器. 因为这会涉及到梯度爆炸, 梯度消失的问题. 因为时间的关系, 我们可能会在以后来具体谈谈这个问题.

最后我们说说, 在具体的例子中, 我们默认首选的激励函数是哪些. 在少量层结构中, 我们可以尝试很多种不同的激励函数. 在卷积神经网络 Convolutional neural networks 的卷积层中, 推荐的激励函数是 relu. 在循环神经网络中 recurrent neural networks, 推荐的是 tanh 或者是 relu (这个具体怎么选, 我会在以后 循环神经网络的介绍中在详细讲解).

---

建造我们第一个神经网络

添加层 def add_layer()

定义 add_layer()

在 Tensorflow 里定义一个添加层的函数可以很容易的添加神经层,为之后的添加省下不少时间.

神经层里常见的参数通常有weights、biases和激励函数。

首先，我们需要导入tensorflow模块。

import tensorflow as tf

然后定义添加神经层的函数def add_layer(),它有四个参数：输入值、输入的大小、输出的大小和激励函数，我们设定默认的激励函数是None。

def add_layer(inputs, in_size, out_size, activation_function=None):    

接下来，我们开始定义weights和biases。

因为在生成初始参数时，随机变量(normal distribution)会比全部为0要好很多，所以我们这里的weights为一个in_size行, out_size列的随机变量矩阵。

Weights = tf.Variable(tf.random_normal([in_size, out_size]))

在机器学习中，biases的推荐值不为0，所以我们这里是在0向量的基础上又加了0.1。

biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)

下面，我们定义Wx_plus_b, 即神经网络未激活的值。其中，tf.matmul()是矩阵的乘法。

Wx_plus_b = tf.matmul(inputs, Weights) + biases

当activation_function——激励函数为None时，输出就是当前的预测值——Wx_plus_b，不为None时，就把Wx_plus_b传到

activation_function()函数中得到输出。

if activation_function is None:

        outputs = Wx_plus_b

    else:

        outputs = activation_function(Wx_plus_b)

最后，返回输出，添加一个神经层的函数——def add_layer()就定义好了。

return outputs

建造神经网络

add_layer 功能

首先，我们导入本次所需的模块。

import tensorflow as tf

import numpy as np

构造添加一个神经层的函数。（在上次课程中有详细介绍）

def add_layer(inputs, in_size, out_size, activation_function=None):

    Weights = tf.Variable(tf.random_normal([in_size, out_size]))

    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)

    Wx_plus_b = tf.matmul(inputs, Weights) + biases

    if activation_function is None:

        outputs = Wx_plus_b

    else:

        outputs = activation_function(Wx_plus_b)

    return outputs

导入数据

构建所需的数据。 这里的x_data和y_data并不是严格的一元二次函数的关系，因为我们多加了一个noise,这样看起来会更像真实情况。

x_data = np.linspace(-1,1,300, dtype=np.float32)[:, np.newaxis]

noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)

y_data = np.square(x_data) - 0.5 + noise

利用占位符定义我们所需的神经网络的输入。 tf.placeholder()就是代表占位符，这里的None代表无论输入有多少都可以，因为输入只有一个特征，所以这里是1。

xs = tf.placeholder(tf.float32, [None, 1])

ys = tf.placeholder(tf.float32, [None, 1])

接下来，我们就可以开始定义神经层了。 通常神经层都包括输入层、隐藏层和输出层。这里的输入层只有一个属性， 所以我们就只有一个输入；隐藏层我们可以自己假设，这里我们假设隐藏层有10个神经元； 输出层和输入层的结构是一样的，所以我们的输出层也是只有一层。 所以，我们构建的是——输入层1个、隐藏层10个、输出层1个的神经网络。

搭建网络

下面，我们开始定义隐藏层,利用之前的add_layer()函数，这里使用 Tensorflow 自带的激励函数tf.nn.relu。

l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)

接着，定义输出层。此时的输入就是隐藏层的输出——l1，输入有10层（隐藏层的输出层），输出有1层。

prediction = add_layer(l1, 10, 1, activation_function=None)

计算预测值prediction和真实值的误差，对二者差的平方求和再取平均。

loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),

                     reduction_indices=[1]))

接下来，是很关键的一步，如何让机器学习提升它的准确率。tf.train.GradientDescentOptimizer()中的值通常都小于1，这里取的是0.1，代表以0.1的效率来最小化误差loss。

train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

使用变量时，都要对它进行初始化，这是必不可少的。

# init = tf.initialize_all_variables() # tf 马上就要废弃这种写法

init = tf.global_variables_initializer()  # 替换成这样就好

定义Session，并用 Session 来执行 init 初始化步骤。 （注意：在tensorflow中，只有session.run()才会执行我们定义的运算。）

sess = tf.Session()

sess.run(init)

训练

下面，让机器开始学习。

比如这里，我们让机器学习1000次。机器学习的内容是train_step, 用 Session 来 run 每一次 training 的数据，逐步提升神经网络的预测准确性。 (注意：当运算要用到placeholder时，就需要feed_dict这个字典来指定输入。)

for i in range(1000):

    # training

    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})

每50步我们输出一下机器学习的误差。

   

if i % 50 == 0:

        # to see the step improvement

        print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))

在电脑上运行本次代码的结果为：

通过上图可以看出，误差在逐渐减小，这说明机器学习是有积极的效果的。

结果可视化

matplotlib 可视化

构建图形，用散点图描述真实数据之间的关系。 （注意：plt.ion()用于连续显示。）

# plot the real data

fig = plt.figure()

ax = fig.add_subplot(1,1,1)

ax.scatter(x_data, y_data)

plt.ion()#本次运行请注释，全局运行不要注释

plt.show()

散点图的结果为：

接下来，我们来显示预测数据。

每隔50次训练刷新一次图形，用红色、宽度为5的线来显示我们的预测数据和输入之间的关系，并暂停0.1s。

for i in range(1000):

    # training

    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})

    if i % 50 == 0:

        # to visualize the result and improvement

        try:

            ax.lines.remove(lines[0])

        except Exception:

            pass

        prediction_value = sess.run(prediction, feed_dict={xs: x_data})

        # plot the prediction

        lines = ax.plot(x_data, prediction_value, 'r-', lw=5)

        plt.pause(0.1)

最后，机器学习的结果为：

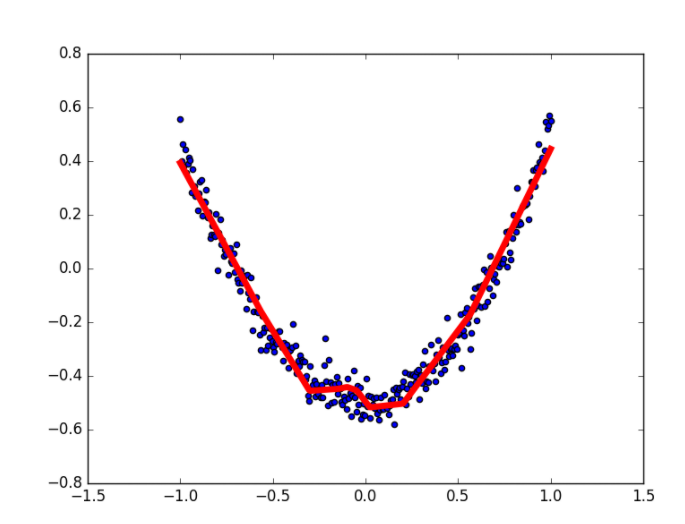
加速神经网络训练 (Speed Up Training)

包括以下几种模式:

Stochastic Gradient Descent (SGD)

Momentum

AdaGrad

RMSProp

Adam

越复杂的神经网络 , 越多的数据 , 我们需要在训练神经网络的过程上花费的时间也就越多. 原因很简单, 就是因为计算量太大了. 可是往往有时候为了解决复杂的问题, 复杂的结构和大数据又是不能避免的, 所以我们需要寻找一些方法, 让神经网络聪明起来, 快起来.

Stochastic Gradient Descent (SGD)

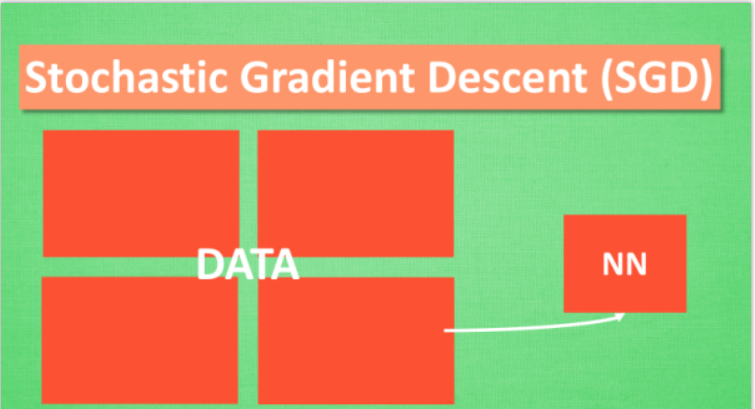
所以, 最基础的方法就是 SGD 啦, 想像红色方块是我们要训练的 data, 如果用普通的训练方法, 就需要重复不断的把整套数据放入神经网络 NN训练, 这样消耗的计算资源会很大.

我们换一种思路, 如果把这些数据拆分成小批小批的, 然后再分批不断放入 NN 中计算, 这就是我们常说的 SGD 的正确打开方式了. 每次使用批数据, 虽然不能反映整体数据的情况, 不过却很大程度上加速了 NN 的训练过程, 而且也不会丢失太多准确率.如果运用上了 SGD, 你还是嫌训练速度慢, 那怎么办?

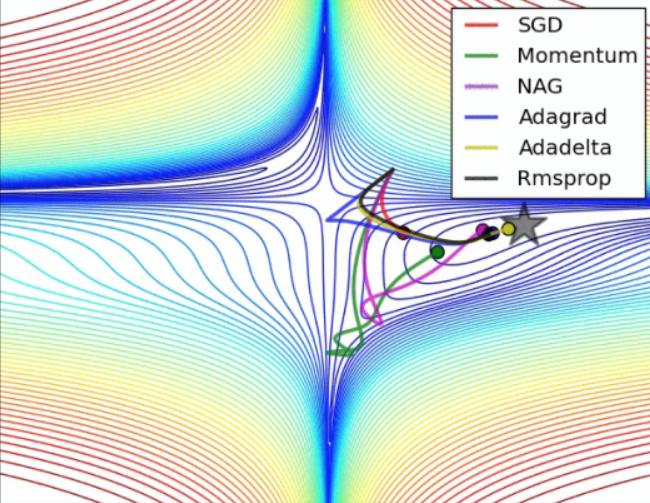
没问题, 事实证明, SGD 并不是最快速的训练方法, 红色的线是 SGD, 但它到达学习目标的时间是在这些方法中最长的一种. 我们还有很多其他的途径来加速训练.

Momentum 更新方法

大多数其他途径是在更新神经网络参数那一步上动动手脚. 传统的参数 W 的更新是把原始的 W 累加上一个负的学习率(learning rate) 乘以校正值 (dx). 这种方法可能会让学习过程曲折无比, 看起来像 喝醉的人回家时, 摇摇晃晃走了很多弯路.

所以我们把这个人从平地上放到了一个斜坡上, 只要他往下坡的方向走一点点, 由于向下的惯性, 他不自觉地就一直往下走, 走的弯路也变少了. 这就是 Momentum 参数更新. 另外一种加速方法叫AdaGrad.

AdaGrad 更新方法

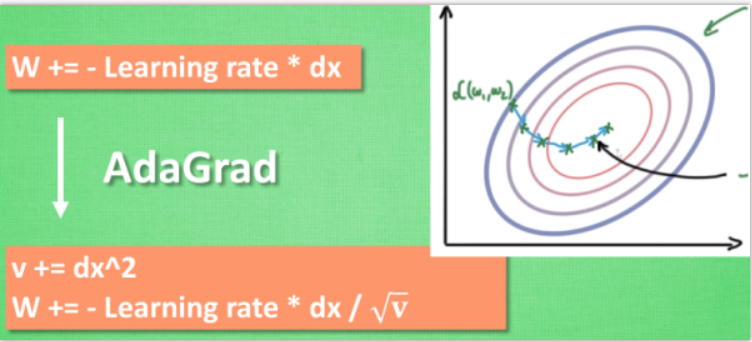
这种方法是在学习率上面动手脚, 使得每一个参数更新都会有自己与众不同的学习率, 他的作用和 momentum 类似, 不过不是给喝醉酒的人安排另一个下坡, 而是给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走. 他的数学形式是这样的. 接下来又有什么方法呢? 如果把下坡和不好走路的鞋子合并起来, 是不是更好呢? 没错, 这样我们就有了 RMSProp 更新方法.

RMSProp 更新方法

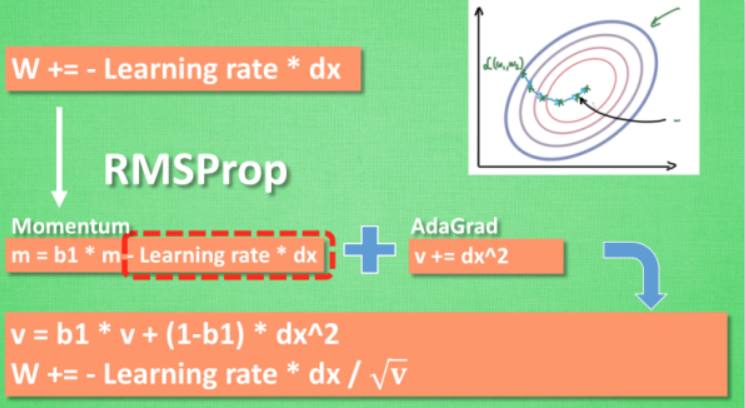
有了 momentum 的惯性原则 , 加上 adagrad 的对错误方向的阻力, 我们就能合并成这样. 让 RMSProp同时具备他们两种方法的优势. 不过细心的同学们肯定看出来了, 似乎在 RMSProp 中少了些什么. 原来是我们还没把 Momentum合并完全, RMSProp 还缺少了 momentum 中的 这一部分. 所以, 我们在 Adam 方法中补上了这种想法.

Adam 更新方法

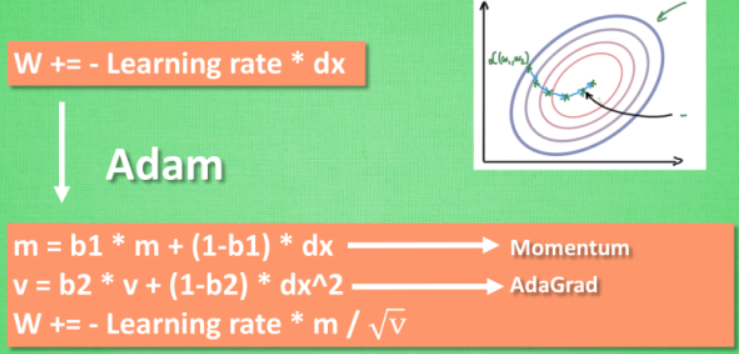
计算m 时有 momentum 下坡的属性, 计算 v 时有 adagrad 阻力的属性, 然后再更新参数时 把 m 和 V 都考虑进去. 实验证明, 大多数时候, 使用 adam 都能又快又好的达到目标, 迅速收敛. 所以说, 在加速神经网络训练的时候, 一个下坡, 一双破鞋子, 功不可没.

优化器 optimizer

各种不同的优化器

本次课程，我们会讲到Tensorflow里面的优化器。

Tensorflow 中的优化器会有很多不同的种类。最基本, 也是最常用的一种就是GradientDescentOptimizer。

在Google搜索中输入“tensorflow optimizer”可以看到Tensorflow提供了7种优化器：链接

代码区：https://github.com/ZhangTongLe/Tensorflow-Tutorial