# 基础知识
# NumPy的主要对象是齐次多维数组。它是一个元素表(通常是数字),所有相同的类型,由正整数的元组索引。在NumPy维度被称为轴。轴的数量是等级。
#
# 例如,三维空间中一个点的坐标[1,2,1]是一个等级为1的数组,因为它具有一个坐标轴。该轴的长度为3.在下面的示例中,该数组具有等级2(它是二维的)。第一维(轴)的长度为2,第二维的长度为3。
#
# [[ 1. , 0. , 0 ],
# [ 0. , 1. , 2. ]]
# NumPy的数组类叫做ndarray。它也被别名数组所知 。请注意,numpy.array与标准Python库类array.array不一样,它只处理一维数组,并且提供较少的功能。ndarray对象的更重要的属性是:
#
# ndarray.ndim
# 阵列的轴数(维度)。在Python世界中,维度的数量被称为等级。
# ndarray.shape
# 数组的尺寸。这是一个整数的元组,指示每个维度中数组的大小。对于有n行m列的矩阵,形状将是(n,m)。形状元组的长度 因此是等级或维数 ndim。
# ndarray.size
# 数组元素的总数。这等于形状的元素的乘积。
# ndarray.dtype
# 一个描述数组中元素类型的对象。可以使用标准的Python类型创建或指定dtype。另外NumPy提供它自己的类型。numpy.int32,numpy.int16和numpy.float64是一些例子。
# ndarray.itemsize
# 数组中每个元素的字节大小。例如,类型为float64的元素的数组具有项目大小 8(= 64/8),而类型complex32中的一个具有项目大小 4(= 32/8)。这相当于ndarray.dtype.itemsize。
# ndarray.data
# 包含数组的实际元素的缓冲区。通常,我们不需要使用这个属性,因为我们将使用索引设施访问数组中的元素。
import numpy as np #可用来存储和处理大型矩阵的工具
from numpy import pi
import matplotlib.pyplot as plt
a = np.arange(15).reshape(3, 5) # 默认是从生成0-14个数字,分成三组,每组5个元素。
a
a.shape #数组的尺寸
a.ndim #阵列的轴数
a.dtype.name #一个描述数组中元素类型的对象
a.itemsize #数组中每个元素的字节大小
a.size #数组元素的总数
type(a)
b = np.array([6, 7, 8]) #创建一个数组
b
b.dtype
type(b) #获取变量b的数据类型
np.array([(1.5, 2, 3), (4, 5, 6)]) #数组将序列序列转换成二维数组,将序列序列转换成三维数组,等等
np.array([[1, 2], [3, 4]], dtype=complex) #数组的类型也可以在创建时明确指定:
#----NumPy提供了几个函数来创建具有初始占位符内容的数组。 这样可以最大限度地减少增加阵列的成本 ----#
np.zeros((3,4)) #创建全是零的二维,三组4列的元素。默认情况下,创建的数组的dtype是float64。
np.ones((2,3,4), dtype=np.int16) #创建全是1的三维数组,分两组,4列。
np.empty((2,3))#空函数创建一个数组,其初始内容是随机的,取决于内存的状态
np.arange(10, 30, 5) #返回一个范围数组数组
np.linspace( 0, 2, 9 ) #arange与浮点参数一起使用时,由于有限的浮点精度,获得不到元素的数量。 使用函数linspace作为参数来接收我们想要的元素的数量
x = np.linspace( 0, 2*pi, 100 ) #用于评估许多点的功能
f = np.sin(x)
np.arange(6) #一维数组
np.arange(12).reshape(4,3) #二维数组
np.arange(24).reshape(2,3,4) #三维数组
np.arange(10000) #如果数组太大而无法打印,NumPy会自动跳过数组的中心部分,只打印角点:
#数组上的算术运算符应用于元素。 一个新的数组被创建并填充结果
a = np.array([20, 30, 40, 50])
b = np.arange(4)
b
a-b
b**2
10*np.sin(a)
a<35
#与许多矩阵语言不同,运算符 *在NumPy数组中以元素形式操作。 矩阵乘积可以使用点函数或方法执行:
A = np.array( [[1,1],[0,1]] )
B = np.array( [[2,0],[3,4]] )
A*B
A.dot(B) #所得到的数组中的每个元素为,第一个矩阵中与该元素行号相同的元素与第二个矩阵与该元素列号相同的元素,两两相乘后再求和。
#A第一行元素:[1,1] * B第一列元素 [2,3] = 1*2 +1*3 = 5 =X = array([[X, Y], [X1, Y1]])
#A第一行元素:[1,1] * B第二列元素 [0,4] = 1*0 +1*4 = 4 =Y = array([[X, Y], [X1, Y1]])
#A第二行元素:[0,1] * B第一列元素 [2,3] = 0*2 +1*3 = 3 =x1 = array([[X, Y], [X1, Y1]])
#A第二行元素:[0,1] * B第二列元素 [0,4] = 0*0 +1*4 = 4 =y1 = array([[X, Y], [X1, Y1]])
# 最终输出结果:array([[5, 4], [3, 4]])
###############################################################################################################
#例如+ =和* =)适当地修改现有数组,而不是创建一个新数组。
a = np.ones((2,3), dtype=int)
b = np.random.random((2, 3))
a *= 3
a
b += a
b
a += b #报错,因为b不会自动转换为整数类型
#在使用不同类型的数组时,结果数组的类型对应于更更精确的数组(称为上传)。
a = np.ones(3, dtype=np.int32)
b = np.linspace(0, pi, 3)
b.dtype.name
c = a+b
c
c.dtype.name
d = np.exp(c*1j) #计算各元素的指数值
d
d.dtype.name
#许多一元运算,比如计算数组中所有元素的总和,都是作为ndarray类的方法来实现的。
a = np.random.random((2,3))
a
a.sum()
a.min()
a.max()
#通过指定轴参数,您可以沿着数组的指定轴应用操作
b = np.arange(12).reshape(3, 4)
b
b.sum(axis=0)#每列的总和
b.min(axis=1)#每行最小的数
b.cumsum(axis=1)#每行的累计和,每行除开头外,第二个数是开头数+本身,进行累计。第三个数=第二个数+第三个数
#常用的数学函数,如sin,cos和exp。 在NumPy中,这些被称为“通用函数”(ufunc)
B = np.arange(3)
B
np.exp(B)
np.sqrt(B)
C = np.array([2., -1., 4.])
np.add(B, C)
#一维数组可以被索引,切片和迭代,就像列表和其他Python序列一样。
a = np.arange(10)**3
a
a[2]
a[2:5]
a[:6:2] = -1000 #相当于[0:6:2] = -1000; 从开始到第6位,独占,每第二个元素设置为-1000
a
a[::-1] #把a反向输出
for i in a:
print(i ** (1 / 3.))
#多维数组每个轴可以有一个索引。 这些索引用逗号分隔: [y的索引:x的索引] =[y+1:x+1]
def f(x,y):
return 10 * x + y
b = np.fromfunction(f,(5,4),dtype=int) #以f函数式创建数组 ,创建整数数组,y轴为5,x轴为4的数组,
b
b[2, 3]#索引是从零开始,y轴=3,x轴为4 的数为=23
b[0:5, 1] #第二列中的每一行,0:5 是从y轴的取值范围,索引:1 相当于x轴的第二列、
b[ : ,1] #相当于b[0:5, 1],不给取值范围,默认去x轴第二列
b[1:3, :] #第二行和第三行中的每一列。
#当提供的索引数量少于轴数时,缺失的索引被认为是完整的切片:
b[-1] #最后一行 相当于b [-1 ,:]
# a 3D array (two stacked 2D arrays)
c = np.array( [[[ 0, 1, 2], [ 10, 12, 13]],[[100,101,102],[110,112,113]]])
c.shape
c[1,...] #同c [1,:,]或c [1]
c[...,2] #与c [:,:,2]相同
#迭代多维数组是相对于第一个轴完成的:
for row in b:
print(row)
#对数组中的每个元素执行操作,可以使用flat属性,该属性是数组中所有元素的迭代器
for element in b.flat:
print(element)
a = np.floor(10*np.random.random((3,4)))
a
a.shape
##数组的形状可以通过各种命令来改变
a.ravel()#返回展开的数组变成一维度。
a.reshape(6,2) #返回具有修改形状的数组,y变成6行,x变成2列。
a.T #返回数组,转置 x和y轴互换。
a.T.shape
a.shape
a.resize((2,6)) #y轴变两行。x轴变6列。
a
a.reshape(3,-1)#y轴变3行。x轴其-1,会自动计算x轴的列数。
#几个阵列可以沿不同的轴堆叠在一起:
a = np.floor(10*np.random.random((2,2)))
a
b = np.floor(10*np.random.random((2,2)))
b
np.vstack((a,b)) #b数组拼接在a数组的y轴的负方向上
np.hstack((a,b)) #b数组拼接在a数组的x轴的正方向上
#函数column_stack将 一维数组作为列叠加到2维数组中。它相当于仅用于一维数组的vstack:
from numpy import newaxis
np.column_stack((a,b)) # 把a的x和b的x轴的第一行和第二行分别拼接。
a = np.array([4.,6.])
b = np.array([3.,8.])
a[:,newaxis] #这允许有一个2D列向量,
np.column_stack((a[:,newaxis],b[:,newaxis]))
np.vstack((a[:,newaxis],b[:,newaxis])) #把a,b的x变成y,然后进行串联拼接
np.r_[1:4, 0, 4]
#使用hsplit,可以通过指定要返回的相同形状的数组的数量,或通过指定分割应该发生之后的列来沿着其横轴拆分数组:
a = np.floor(10*np.random.random((2,12)))
a
np.hsplit(a, 3) # 沿着x轴拆分成3列(4,4,4)
np.hsplit(a,(3,4)) # 沿着x轴拆分成3列,然后再把第四列拆分为一组。由(4,4,4)变(3,1,8)
#当操作和操作数组时,它们的数据有时会被复制到一个新的数组中,这通常是初学者混淆的来源。有三种情况:
a = np.arange(12)
b = a # 不创建新对象
b is a
b.shape = 3, 4 ##改变形状
a.shape
#Python将可变对象作为引用传递,所以函数调用不会复制。
def f(x):
print(id(x))
id(a) #id是对象的唯一标识符
f(a)
c = a.view()
c is a
c.base is a #c是由拥有的数据的视图
c.flags.owndata
c.shape = 2,6 # 一个的形状不改变
a.shape
c[0,4] = 1234 # a的数据变化
a
s = a[ : , 1:3]
# 为了清晰起见,添加了#个空格; 也可以写成“s = a [:,1:3]”
s[:] = 10 #s [:]是s的视图。注意S = 10和s之间的差[:] = 10
a
#########深复制;该复制方法使阵列及其数据的完整副本。############
d = a.copy() #创建新数据的新数组对象
d is a
d.base is a # d不与分享任何
d[0,0] = 9999
a
#常用的函数大全
# 数组创建
#--- arange, array, copy, empty, empty_like, eye, fromfile,
#--- fromfunction, identity, linspace, logspace, mgrid, ogrid, ones, ones_like,
#--- r, zeros, zeros_like
#转换
#--- ndarray.astype, atleast_1d, atleast_2d, atleast_3d, mat
# 手法
# --- array_split, column_stack, concatenate, diagonal, dsplit,dstack, hsplit, hstack,
# --- ndarray.item, newaxis, ravel, repeat, reshape, resize,
# --- squeeze, swapaxes, take, transpose, vsplit, vstack
#问题
#--- all, any, nonzero, where
# 函数指令
#--- argmax, argmin, argsort, max, min, ptp, searchsorted, sort
# 操作
#--- choose, compress, cumprod, cumsum, inner, ndarray.fill, imag, prod, put, putmask, real, sum
# 基本统计
#--- cov, mean, std, var
# 基本的线性代数
#--- cross, dot, outer, linalg.svd, vdot
# Numpy的API
a = np.arange(12)**2 # 前12个平方数
i = np.array( [ 1,1,3,8,5 ] ) # 一个索引的阵列
a[i] # 的在位置上的元件我
j = np.array( [ [ 3, 4], [ 9, 7 ] ] ) # 索引的二维阵列
a[j] # 相同的形状为J
# -----当索引数组a是多维时,单个索引数组指向a的第一维。 以下示例通过使用调色板将标签图像转换为彩色图像来显示此行为。--------#
palette = np.array( [ [0,0,0], # 黑色
[255,0,0], # 红色
[0,255,0], # 绿色
[0,0,255], # 蓝色
[255,255,255] ] ) # 白色
image = np.array( [ [ 0, 1, 2, 0 ], # 每一值对应于在调色板中的颜色
[ 0, 3, 4, 0 ] ] )
palette[image] # (2,43)彩色图像
# 可以给一个以上的维度指标。每个维度的索引数组必须具有相同的形状。
a = np.arange(12).reshape(3,4)
a
i = np.array( [ [0,1], # 用于第一暗淡的指数
[1,2] ] )
j = np.array( [ [2,1], # 第二个暗淡的指数
[3,3] ] )
a[i,j] #i和j必须具有相同的形状,a(0,2) =2 a(1,1)=5 ,a(1,3) =7 ,a(2,3) =11 最终结果-->array([[ 2, 5],[ 7, 11]])
a[i,2]#i和j必须具有相同的形状,a(0,2) =2 a(1,2)=6 , a(1,2)=6 ,a(2,2) =10 最终结果-->array([[ 2, 6], [ 6, 10]])
a[:,j] # i.e., a[ : , j]
# 可以把i和j放在一个序列中(比如说一个列表),然后用列表进行索引。
l = [i,j]
a[l] # 等同于[i,j]
s = np.array([i,j])
a[s] # 出错,不能通过将i和j放入一个数组。
a[tuple(s)] # 相同作为[i,j]
# 数组索引的另一个常见用途是搜索时间相关系列的最大值:
time = np.linspace(20, 145, 5) # 时标
data = np.sin(np.arange(20)).reshape(5,4) # 4随时间变化的一系列
time
data
ind = data.argmax(axis=0) # 每个系列最大值的索引
ind
time_max = time[ind] # 对应于最大值的次数
data_max = data[ind, range(data.shape[1])] # => data[ind[0],0], data[ind[1],1]...
time_max
data_max
np.all(data_max == data.max(axis=0))
# 使用数组的索引作为分配给的目标:
a = np.arange(5)
a
a[[1,3,4]] = 2
a
# 当索引列表包含重复时,分配会执行好几次,而留下最后一个值
a = np.arange(5)
a #输出array([0, 1, 2, 3, 4])
#索引0 更为为1,第二次索引更改为2,所以数组的a处的零索引取值为原数组的为2索引的值:2 ,然后索引2处的数改为索引3的数,
a[[0,0,2]]=[1,2,3]
a
# 这足够合理,但要小心如果你想使用Python的 + =构造,因为它可能不会做你期望的:
a = np.arange(5)
a[[0,0,2]]+=1
a
# 布尔索引最自然的方法就是使用与原始数组形状相同的布尔数组:
a = np.arange(12).reshape(3,4)
b = a > 4
b # b为具有的形状的布尔
a[b] # 一维数组与选定的元素
# 这个属性在作业中非常有用:
a[b] = 0 #'A'大于4的所有元素用零代替
a
# 使用布尔索引来生成Mandelbrot集的图像:
def mandelbrot( h,w, maxit=20 ):
"""返回Mandelbrot分形的图像大小(h,w )."""
y,x = np.ogrid[ -1.4:1.4:h*1j, -2:0.8:w*1j ]
c = x+y*1j
z = c
divtime = maxit + np.zeros(z.shape, dtype=int)
for i in range(maxit):
z = z**2 + c
diverge = z*np.conj(z) > 2**2 # 正在发偏离的人
div_now = diverge & (divtime==maxit) # 现在偏离的人
divtime[div_now] = i # 注意何时
z[diverge] = 2 # 避免偏离太多
return divtime
plt.imshow(mandelbrot(400,400))
plt.show()
# 用布尔值编制索引的第二种方法更类似于整数索引; 对于数组的每个维度,我们给出一个1D布尔数组,选择我们想要的切片:
a = np.arange(12).reshape(3,4)
a
b1 = np.array([False,True,True]) # 第一个dim选择
b1
b2 = np.array([True,False,True,False]) # 第二个dim选择
b2
a[b1,:] # 选择行(b1([False, True, True]),第一行不显示
a[b1] # 一样
a[:,b2] # 选择列
a[b1,b2] # 一个奇怪的事情要做
# ix_()函数:该ix_函数可用于不同的载体结合,以便获得对于每一个n-uplet结果。
# 例如,如果要计算从每个矢量a,b和c取得的所有三元组的所有a + b * c:
a = np.array([2,3,4,5])
b = np.array([8,5,4])
c = np.array([5,4,6,8,3])
ax,bx,cx = np.ix_(a,b,c)
ax
bx
cx
ax.shape, bx.shape, cx.shape
result = ax+bx*cx
result
# 你也可以按如下方式执行reduce:
def ufunc_reduce(ufct, *vectors):
vs = np.ix_(*vectors)
r = ufct.identity
for v in vs:
r = ufct(r,v)
return r
ufunc_reduce(np.add,a,b,c)
# 用字符串索引
# 线性代数
a = np.array([[1.0, 2.0], [3.0, 4.0]])
a
a.transpose() #x,y转换
np.linalg.inv(a)
u = np.eye(2) # 2×2矩阵; “眼睛”代表“我”
u
j = np.array([[0.0, -1.0], [1.0, 0.0]])
np.dot (j, j) # 矩阵产品
np.trace(u) # 返回数组的对角线的和。
y = np.array([[5.], [7.]])
np.linalg.solve(a, y)
np.linalg.eig(j)
# 参数:
# 方矩阵
# 返回
# 特征值,每个特征根据其多重性重复。
# 归一化的(单位“长度”)特征向量,
# 列`
v [:,i]是对应的特征向量# 特征值`
w [i]`。# 技巧和提示: 要更改数组的尺寸,可以省略其中一个尺寸,然后自动推导出这些尺寸
a = np.arange(30)
a.shape = 2,-1,3 # -1表示“任何需要”
a.shape
a
# 矢量堆叠
x = np.arange(0,10,2) # x=([0,2,4,6,8])
y = np.arange(5) # y=([0,1,2,3,4])
m = np.vstack([x,y]) # m=([[0,2,4,6,8],
# [0,1,2,3,4]])
xy = np.hstack([x,y]) # xy =([0,2,4,6,8,0,1,2,3,4])
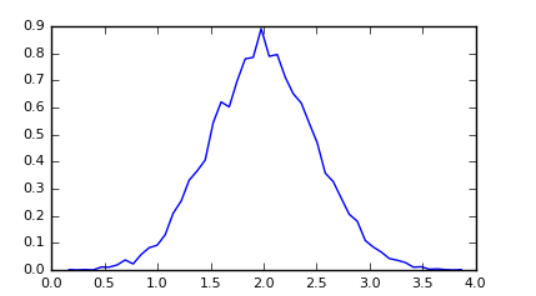
# 直方图
# #构建10000个正常偏离的矢量方差0.5 ^ 2和平均2
mu, sigma = 2, 0.5
v = np.random.normal(mu,sigma,10000)
# #绘制一个规格化的直方图与50箱
plt.hist(v, bins=50, normed=1) # matplotlib版本(图)
plt.show()
# #用numpy计算直方图,然后绘制
(n, bins) = np.histogram(v, bins=50, normed=True) # #NumPy版本(无图)
plt.plot(.5*(bins[1:]+bins[:-1]), n)
plt.show()
 同乐学堂
同乐学堂
 微信扫一扫,打赏作者吧~
微信扫一扫,打赏作者吧~






